Cyclization versus Linear Polymerization

The first theories of step-growth polymerization (SGP) were developed by Carothers, Arvin, Natta, and Dorough in the 1930th.1-5 Carothers and coworkers realized early on that in any step-growth polymerization, the formation of linear polymers competes with cyclization reactions. For example, the reaction of an A-B type monomer such as a hydroxy acid, may produce cyclic esters via intramolecular cyclization during any stage of polymerization and at any concentration:

whereas condensation of A-A type monomers with B-B type monomers yields mainly oligomers, because intermolecular ring formation is considered not very probable. The difunctional oligomers, however, can also undego cyclization reactions. For example, esterification of a dibasic acid with a dihydric alcohol yields A-B type oligomers. Once linear step-growth has reached the dimer or trimer stage, intramolecular cyclization can occur as well:

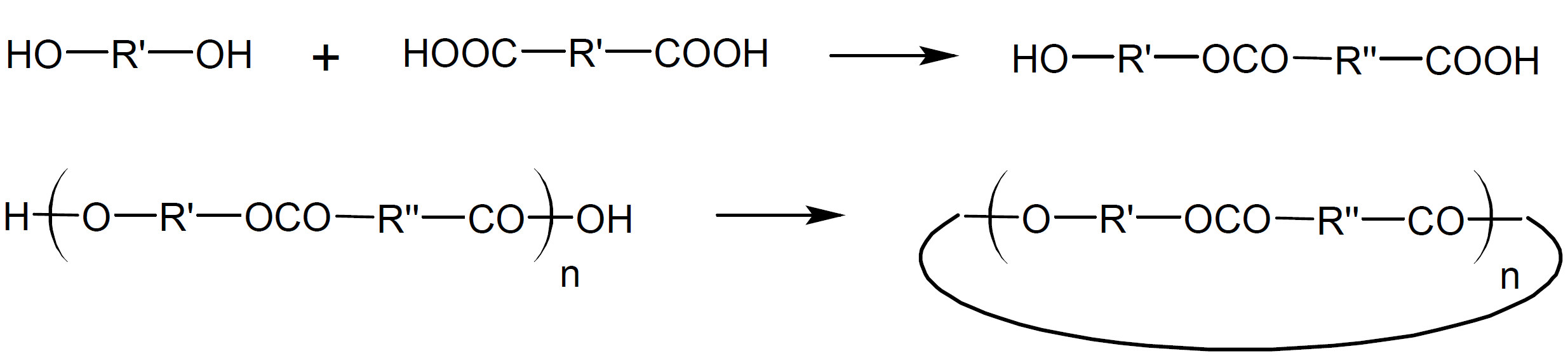
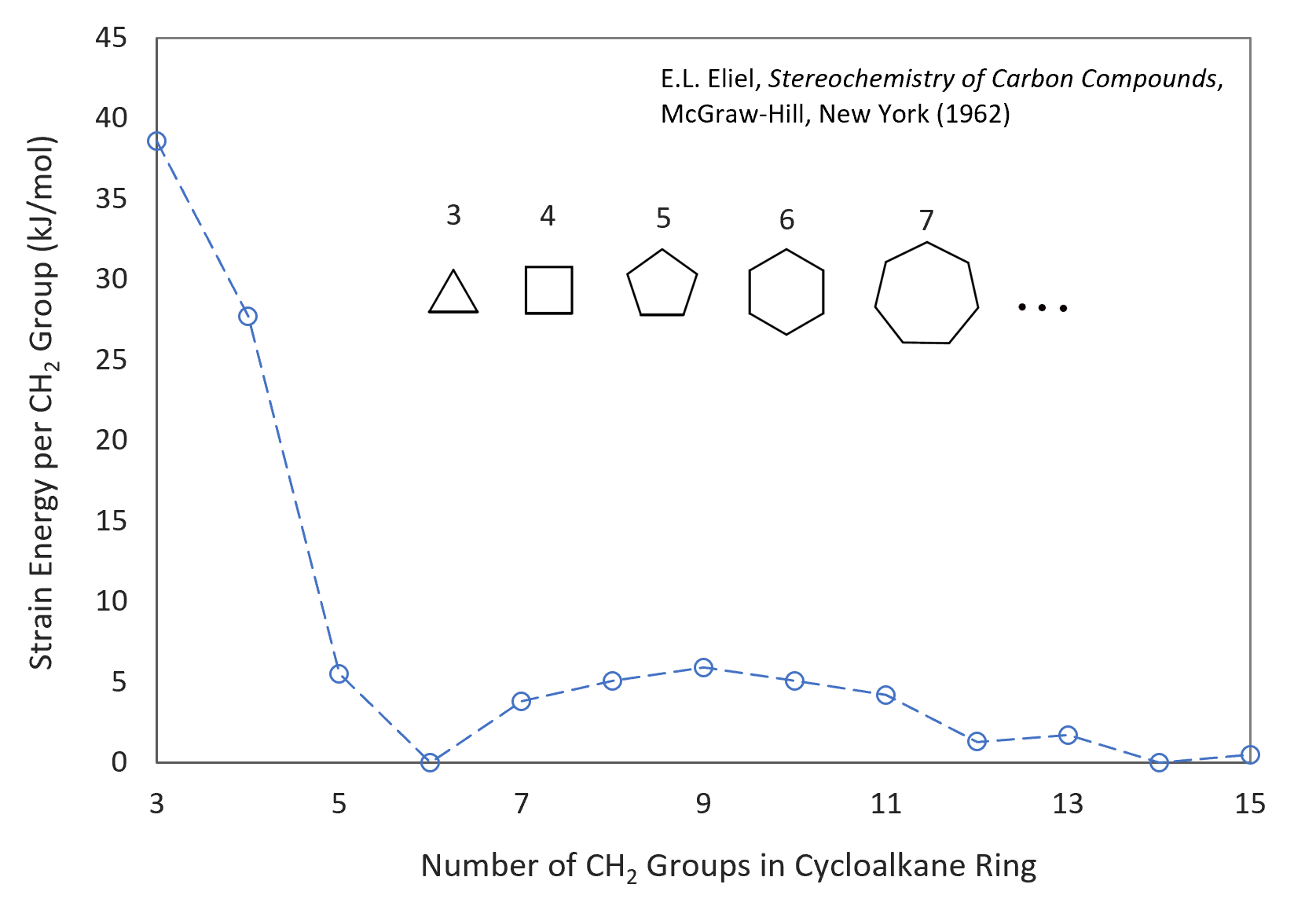
The main factors that control the size and number of rings formed during polycondensation are ring-strain, monomer concentration, and degree of conversion. Ring-strain is the most important factor in the early stages of a SGP when only small rings via intramolecular condensation are formed. The stability of rings decreases with increasing strain in the ring structure. The strain in cyclic rings with less than five atoms is typically very high. Thus, the formation of these rings is energetically very unfavorable. For this reason, A-B type bifunctional monomers of less than five atoms will consist almost entirely of linear structures. If, on the other hand, a bifunctional monomer such as hydroxy or  amino acid consists of 5, 6, or 7 atoms, ring-strain is typically much lower so that both rings and linear structures can be formed, and if the ring strain is close to zero, cyclic monomers will prevail over linear bifunctional monomers.6 For rings of about 8 - 12 atoms, ring strain will remain relative large. This was explained by forced crowding of substituents within the interior of the rings (transannular strain7) which results in strong repulsive interaction of ring substituents on non-adjacent carbons which greatly reduces the probability of ring formation. For rings with more than 13 ring atoms, bond angle distortion is small or negligible and the substituents are mainly in eclipsed configurations. Thus, the strain in carbon rings decreases in the order 3; 4 < 5; 7-11 < 12; 13 < 6 and larger (see figure below). A similar order of stability is observed for many other ring structures including groups other than methylene such as oxygene and nitrogene.

 

Strain Energy of Cycloalkanes

As has been shown by Jacobson, Stockmayer and Flory, the fraction of rings formed during a condensation reaction also depends on the concentration of reactive groups (dilution) and chain length.6,9 The probability of ring formation decreases with increasing molecular weight because there are fewer opportunities for the functional groups at the ends of the chain to meet and cyclize whereas an increase in monomer concentration has the opposite effect, because there are more opportunities for intermolecular chain growth than for intramolecular cyclization. A (semi-)quantitative explanation of the observed concentration dependence was given by Flory (1953):.6 Assuming the concentrations of the two reactive groups are stoichiometric, [A] = [B] = [M], as is the case for byfunctional monomers, the rate of cyclization is given by kc [M] and the rate of linear step-growth by kl [M]2, where kc and kl are the rate constants for cyclization and intermolecular step-growth, respectively. Then the ratio R of cyclic structures to linear chains is inversely proportional to the concentration of reactive groups [M]:

R = kc / kl [M] = C / [M]

The cyclization constant C may be calculated from the observed ratio of the two products at a given concentration [M]. Generally, the decrease in kc with increasing ring size is much greater than the decrease in [M] so that ordinary bifunctional condensation of more than seven atoms does not yield rings in appreciable amount.6

Kricheldorf and Schwarz10 pointed out that the classic theories of step-growth polymerization do not distinguish between kinetically controlled (KCP) and thermodynamically controlled (TCP) polymerization. Thermodynamically controlled SGP involves (rapid) equilibration reactions including ring-chain and ring-ring equilibria throughout the polymerization, so that the reaction mixture condenses to the thermodynamically most favorable distribution at any stage of reaction. According to Kricheldorf and coworkers, most cyclic oligomers are formed by backbiting reactions, which proceed by intramolecular (interchange) substitution from the most reactive chain end.12-13 For example, the terminal hydroxyl groups of a polyester chain can react with one of its ester carbonyl groups yielding cyclic oligoesters in addition to hydroxyl terminated linear chains:

Thus, in a thermodynamically controlled polymerization, cyclic structures are formed at almost all stages of the polymerization.

In a kinetically controlled SGP, equilibration reactions are completely absent, so that the mixture of mers does not reach its thermodynamically most favorable distribution. However, very few condensation reactions are kinetically controlled. Examples of this type of SGP include the reactions of a dicarboxylic acid dichloride with a diol or diamine. These reactions proceed very rapidly without equilibriation. Polymers obtained by KCP have typically a wider molecular weight distribution than polymers produced by equilibrium methods.

In the absence of side reactions and perfect stoichiometry, the molar fraction of cycles should approache 100 % regardless of the initial monomer concentration and process conditions. However, in conventional step polymerization, 100% conversion cannot be achieved and the mixture of products will always contain some (fraction of) percentage of linear chains whereas conventional step-growth polymerization at high monomer concentration and moderate conversion yields mostly linear chains.14 However, even a small amount of low molecular weight cyclic structures can be detrimental to the performance. For this reason, cyclic compounds are often removed from the product by extraction, distillation etc.

 

Notes & References:

  1. Wallace H. Carothers, J. Am. Chem. Soc., 51 (8), pp. 2548-2559 & 51 (8); pp 2560-2570 (1929), 52 (1); pp. 314-326 & 52 (2), pp. 711-721 (1930)

  2. W.H. Carothers, and F.J. Van Natta, J. Am. Chem. Soc., 52 (1); pp. 314-326 (1930)

  3. W.H. Carothers, and G.L. Dorough, J. Am. Chem. Soc., 52 (2), pp. 711-721 (1930)

  4. F.J. van Natta, J.W. Hill & W.H. Carothers, J. Am. Chem. Soc., 56 (2), pp. 455-457 (1934)

  5. P.J. Flory, Chem. Rev., 39 (1), 137 - 197 (1946)

  6. Paul L. Flory, Principles of Polymer Chemistry, Ithaca, New york, 1953

  7. The strain in rings results from a combination of angle distortion, unfavorable bond twisting (torsional-eclipsing), and increased van-der Waals interaction between the atoms in the ring structure. If the bond angles deviate from the normal (tetrahedral) values in the linear chain, internal strain is imposed on the rings which is known as Bayer strain. This type of strain energy is very large in rings of less than five atoms and can reach values of 30 to 40 kJ/mol per atom in 3- to 4-member rings but is only 5 to 7 kJ/mol for hetero-rings of 5 to 7 atoms (cyclic esters).8 Torsional strain occurs when atoms separated by three bonds assume an eclipsed conformation rather than the more stable staggered conformation. The torsional strain in cyclic molecules due to bond twisting is called Pitzer strain. The barrier of rotation between staggered conformations is typically in the range of 2.0 kJ/mol/ (PE). Rings of 7 to 13 carbon atoms experience more strain energy than cyclohexane, largely due to energetically unfavorable torsional arrangements. The third type of strain, the transannular strain or Prelog strain, arises from the repulsive interactions of ring substituents on non-adjacent carbons due to lack of space in the interior of the ring structure. In medium-sized rings of about 8 to 11 atoms, transannular strain can make a major contribution to the overall strain, especially in conformations that experience noticeable Pitzer strain as well. In larger rings (≥ 14), transannular strain practically disappears because the rings become sufficiently large enough to accommodate ring substituents without causing any major transannular repulsions.

  8. W. Saiyasombat, R. Molloy, T.M. Nicholson, A.F. Johnson, I.M. Ward & S. Poshyachinda, Polymer, Vol. 39 (23), pp. 5581-5585 (1998)

  9. H. Jacobson & W. H. Stockmayer, J. Chem. Phys., 18, 1600-6 (1950)

  10. H.R. Kricheldorf & G. Schwarz, Macromol. Rapid Commun., 24, No. 5/6, 359 - 381 (2003)

  11. Korshak, Pure Appl. Chem., 12, 101 - 115 (1966)

  12. H.R. Kricheldorf, Macromol. Rapid Commun., 30, 1371-1381 (2009)

  13. H.R. Kricheldorf, J. Polym. Sci. Part A: Polym. Chem.: Vol. 48, 251-284 (2010)

  14. Step polymerization reactions at moderate conversions yield mainly linear polymers unless rings of size 5 to 7 can be formed, as it is the case for some difunctional monomers.1,6  

  • Summary

  • Cyclization vs. Polymerization

    At any stage of a step-growth polymerization and at any monomer concentration, the formation of linear polymers competes with intramolecular cyclization reations.

  • According to Flory's equal reactivity principle, the reactivity of the end groups is independent of the size of the oligomers, whereas the rate of cyclization greatly depends on the size of the difunctional oligomers.

  • The main factors that control the size and number of rings formed by intramolecular condensation are ring-strain, chain stiffness, monomer/oligomer concentration, stoichiometric ratio or imbalance, and conversion.

  • The strain in cyclic rings with less than five atoms is typically very high. Therefore, the formation of rings with three or four atoms is energetically very unfavorable.

  • Rings consisting of 5, 6 or 7 atoms typically have low ring-strain so that both rings and linear structures can be formed from A-B type monomers.

  • Condensation reactions involving 8 to 12  atoms do not yield rings in appreciable amount because these rings are formed with exceptional difficulty, even at low monomer concentrations.6

  • A thermodynamically controlled polymerization (TCP) undergoes (rapid) equilibration reactions including ring-chain and ring-ring equilibria so that the mixture assumes its thermodynamically most favorable state.

  • The most common type of equilibration reaction is the reversible formation of cyclic monomers and oligomers via
    back-biting.

  • In a kinetically-controlled step polymerization (KCP), equilibration reactions are completely absent so that the mixture of mers does not reach its thermodynamically most favorable distribution.

  • in a typical KCP, cyclization reactions compete with chain growth at any stage of the polycondensation and at all concentrations.

  • With increasing conversion, more and more cycles will be formed and at conversions beyond 99 % rings will dominate and at 100 % conversion, the mixture will entirely consist of cyclic polymers.13